در این بخش از مقاله آموزش کاتلین به بررسی روش ایجاد تابعهای بازگشتی در این زبان برنامهنویسی میپردازیم. «تابع بازگشتی» (Recursive Function) به تابعی گفته میشود که خودش را فراخوانی کند. همچنین با مفهوم تابع «بازگشتی انتهایی» (Tail Recursion) در کاتلین آشنا خواهیم شد.
چنان که اشاره کردیم تابعی که خودش را فراخوانی کند، تابع بازگشتی نامیده میشود و این تکنیک به طور کلی به نام «بازگشت» (recursion) خوانده میشود. یک مثال فیزیکی از این پدیده را میتوان در زمان قرار دادن دو آینه در روبروی هم مشاهده کرد. هر شیئی که در میان این دو آینه قرار داشته باشد به صورت بازگشتی در آنها بازتاب مییابد.
طرز کار بازگشت در برنامهنویسی چگونه است؟
fun main(args: Array<String>) { ... .. ... recurse() ... .. ...
}
fun recurse() { ... .. ... recurse() ... .. ...
}در کد فوق تابع ()recurse از داخل خود بدنه تابع ()recurse فراخوانی میشود. طرز کار آن به صورت زیر است:
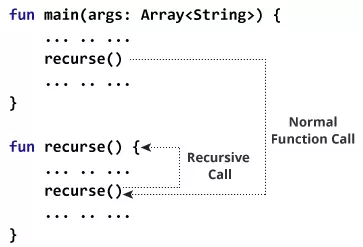
در تصویر فوق میبینیم که فراخوانی بازگشتی تا ابد ادامه مییابد و موجب بروز بازگشت نامتناهی میشود. برای جلوگیری از بازگشت نامتناهی از گزاره if…else (یا رویکردهای مشابه) استفاده میشود که در یک شاخه از آن فراخوانی بازگشتی انجام مییابد و در شاخه دیگر (حصول شرایط مطلوب) متوقف میشود.
مثالی از یافتن فاکتوریل عدد با استفاده از بازگشت در کاتلین
fun main(args: Array<String>) { val number = 4 val result: Long result = factorial(number) println("Factorial of $number = $result")
}
fun factorial(n: Int): Long { return if (n == 1) n.toLong() else n*factorial(n-1)
}خروجی برنامه فوق به صورت زیر است:
Factorial of 4 = 24
طرز کار برنامه فوق چگونه است؟
فراخوانی بازگشتی تابع ()factorial را میتوان با استفاده از تصویر زیر توضیح داد:

مراحل اجرای برنامه فوق به صورت زیر است:
factorial(4)// 1st function call. Argument: 4 4*factorial(3)// 2nd function call. Argument: 3 4*(3*factorial(2))// 3rd function call. Argument: 2 4*(3*(2*factorial(1)))// 4th function call. Argument: 1 4*(3*(2*1)) 24
بازگشت انتهایی در کاتلین
«بازگشت انتهایی» (Tail Recursion) یک مفهوم عمومی است و یک ویژگی زبان کاتلین محسوب نمیشود. برخی زبانهای برنامهنویسی شامل کاتلین از آن برای بهینهسازی فراخوانیهای بازگشتی استفاده میکنند، در حالی که برخی زبانهای دیگر (مانند پایتون) از آنها پشتیبانی نمیکنند.
بازگشت انتهایی در کاتلین چیست؟
در روش معمول اجرای الگوریتمهای بازگشتی، ابتدا همه فراخوانیهای بازگشتی صورت میگیرد و سپس نتیجه از روی مقادیر قبلی در انتها محاسبه میشود. این شیوه در تصویر فوق توصیف شده است. از این رو تا زمانی که همه فراخوانیهای بازگشتی اجرا نشده باشند، نتیجه به دست نمیآید.
اما در فراخوانی بازگشتی انتهایی، محاسبات ابتدا اجرا میشوند و سپس فراخوانیهای بازگشتی اجرا میشوند. به این ترتیب فراخوانی بازگشتی، نتیجه اجرای گام قبلی را به فراخوانی بازگشتی بعدی ارائه میکند. این امر موجب میشود که فراخوانی بازگشتی معادل اجرای حلقه باشد و از خطر بروز «سرریز پشته» (stack overflow) جلوگیری میکند.
شرط بازگشت انتهایی
یک تابع بازگشتی در صورتی برای اجرا به صورت بازگشت انتهایی مناسب است که فراخوانی تابع به خودش، آخرین عملیاتی باید که اجرا میکند. به مثال زیر توجه کنید.
- مثال اول
تابع زیر برای اجرا به صورت «بازگشت انتهایی» مناسب نیست، زیرا فراخوانی تابع به خودش یعنی خط (n*factorial(n-1، آخرین عملیات آن محسوب نمیشود.
fun factorial(n: Int): Long {
if (n == 1) { return n.toLong() } else { return n*factorial(n - 1) }
}- مثال دوم
تابع زیر برای اجرا به صورت بازگشت انتهایی مناسب است، زیرا فراخوانی تابع به خودش یعنی fibonacci(n-1, a+b, a) آخرین عملیات آن است.
fun fibonacci(n: Int, a: Long, b: Long): Long { return if (n == 0) b else fibonacci(n-1, a+b, a)
}برای این که به کامپایلر اعلام کنیم که یک تابع بازگشتی را در کاتلین به صورت بازگشت انتهایی اجرا کند، باید تابع را با مادیفایر tailrec مشخص سازیم.
مثالی از بازگشت انتهایی
import java.math.BigInteger
fun main(args: Array<String>) { val n = 100 val first = BigInteger("0") val second = BigInteger("1")
println(fibonacci(n, first, second))
}
tailrec fun fibonacci(n: Int, a: BigInteger, b: BigInteger): BigInteger { return if (n == 0) a else fibonacci(n-1, b, a+b)
}خروجی کد فوق به صورت زیر است:
354224848179261915075
این برنامه صدمین جمله سری فیبوناچی را محاسبه میکند. از آنجا که خروجی ممکن است عدد صحیح بسیار بزرگی باشد، باید از کلاس BigInteger در کتابخانه استاندارد جاوا کمک بگیریم. در مثال فوق، تابع ()fibonacci با مادیفایری به نام tailrec مشخص شده است و از این رو امکان اجرای بازگشت انتهایی را دارد. به این ترتیب کامپایلر فرایند بازگشتی را در این حالت بهینهسازی میکند.
اگر تلاش کنید جمله 20،000 (یا هر عدد صحیح بزرگ دیگر) سری فیبوناچی را بدون بازگشت انتهایی محاسبه کنید، کامپایلر یک استثنا به صورت java.lang.StackOverflowError ایجاد میکند. با این حال، برنامه ما بدون هیچ مشکلی کار میکند. دلیل این امر آن است که ما از بازگشت انتهایی استفاده کردهایم که از یک حلقه بهینه بر مبنای نسخهای از بازگشت سنتی استفاده میکند.
مثالی از فاکتوریل با استفاده از بازگشت انتهایی
مثال فوق برای محاسبه فاکتوریل یک عدد (مثال اول) را نمیتوان برای اجرا به صورت بازگشت انتهایی بهینهسازی کرد. اما برنامه زیر همین وظیفه را به روش متفاوتی اجرا میکند.
fun main(args: Array<String>) { val number = 5 println("Factorial of $number = ${factorial(number)}")
}
tailrec fun factorial(n: Int, run: Int = 1): Long { return if (n == 1) run.toLong() else factorial(n-1, run*n)
}خروجی برنامه فوق به صورت زیر است:
Factorial of 5 = 120
کامپایلر میتواند در این برنامه فرایند بازگشتی را به صورت یک تابع بازگشتی که امکان اجرای بازگشت انتهایی دارد، بهینهسازی کند و ما از مادیفایر tailrec استفاده کردهایم که موجب بهینهسازی بازگشت از سوی کامپایلر میشود.